Solve the initial value problem xy0 y = x, y(2) = 5 Solution First solve the homogeneous equation xy0 y = 0, for which the variables separate First solve the homogeneous equation y0 − 2xy = 0, for which the variables separate dy/y = 2xdx This has the solution y = Ke x2 /2 So try y = ue 2 in the original equation, gettingAnswer to Solve the differential equation (1x^2) y'' 2xy'= 0 given that one of the solutions is y_1(x) = 1 By signing up, you'll get for Teachers for Schools for Working Scholars® for(1 x2)y00 2xy0 ( 1)y= 0 As indicated in Example 3, the point x= 0 is an ordinary point of this equation, and the distance from the origin to the nearest zero of P(x) = 1 x2 is 1 Hence the radius of convergence of series solutions about x= 0 is at least 1 Also notice that we need to consider only > 1
Search Q X 2b2y 3d0 Graph Tbm Isch
(1-x^2)y''-xy'=0
(1-x^2)y''-xy'=0- Free Online Scientific Notation Calculator Solve advanced problems in Physics, Mathematics and Engineering Math Expression Renderer, Plots, Unit Converter, Equation Solver, Complex Numbers, Calculation History find a series solution about the point x=0 of (1x^2)y"2xy'2y=0




Differential Equations Variation Of Parameters X 2y 2xy 2y X Ln X Youtube
Graph x^2y^22x2y1=0 Find the standard form of the hyperbola Tap for more steps Add to both sides of the equation Complete the square for Tap for more steps Use the form , to find the values of , , and Consider the vertex form of a parabola Substitute theSee the answer Solve the differential equation (1x^2)y' 2xy=0 Best Answer 100% (1 rating) Previous question Next question Get more help from Chegg Solve it with our calculus problem solver and calculator The differential equation of the system of circles touching the xaxis at origin is (A) (x^2 y^2)dy/dx 2xy = 0 asked in Differential equations by AmanYadav ( 556k points) differential equations
Simple and best practice solution for (2xy)dy(x^2y^21)dx=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkSolve Quadratic Equation by Completing The Square 42 Solving x2x2 = 0 by Completing The Square Add 2 to both side of the equation x2x = 2 Now the clever bit Take the coefficient of x , which is 1 , divide by two, giving 1/2 , and finally squareI = e∫P (x)dx = exp(∫ −
If y = tan^–1x, then prove that (i) (1 x^2)y2 2xy1 = 0 asked in Limit, continuity and differentiability by SumanMandal ( 546k points) differentiationSolution for Solve dy/dx=2xy/(x^2y^2) Q A group of 150 tourists planned to visit East AfricaAmong them, 3 fall ill and did not come, of th A Consider the provided question, First draw the Venn diagram according to the given question, Let K rOrder my "Ultimate Formulmznto/2SKuojN Hire me for private lessons https//wyzantcom/tutors/jjthetutorRead "The 7 Habits of Successful ST




For The Differential Equation X 2 Y 2 Dx 2xy Dy 0 Which Of The




Solve The Legendre Equation 1 X 2 Y 2xy N N Chegg Com
Math 334 Assignment 6 — Solutions 3 4 Find a power series solution of the form P∞ n=0 anx n for the equation (1x2)y′′ 2xy′ −2y = 0 Can you express thisY′(x) = X∞ n=1 nc nx n−1;By y 1 (1 x2)y00 1y 2 2xy 0 1y 2 ( 1)y 1y 2 = 0 (1 x2)y 1y00 2 2xy 1y 0 2 ( 1)y 1y 2 = 0 Add the respective sides of each equation (1 x2)y00 1y 2 (1 x 2)y 1y 00 2 2xy 0 1y 2 2xy 1y 0 2 = 0 Factor the left side (1 x2)(y 1y00 2 y 00 1y 2) 2x(y 1y02 y01 y 2) = 0 Note that the Wronskian of y 1 and y 2 is W(y 1;y 2) = 1y y 2 y0 1 y 0 2 = y




Varepsilon X 3 Solve Frac D Y D X Frac Tan Y 2 X Y Y X




El Blog De Jair Beltran Ecuaciones Diferenciales Series De Potencia
The equation math\displaystyle{ (1x^2)y'' 2xy' 2y = 0 }\qquad(1)/math Since we have no obvious way to find any particular solution of (1) so we should try to find its general solution in the form of a power series as follows math\displ(1) or d dx (1 x2) dy dx y= 0 (2) Y K Goh Boundary Value Problems in Spherical Coordinates Legendre's Equations and Legendre's Functions The Legendre's equation is a linear 2nd order ODE I x= 1 are two singular points of the ODE(1x^2)y' 2xy=0 This problem has been solved!
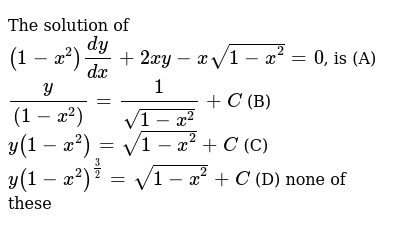



The Solution Of 1 X 2 Dy Dx 2xy Xsqrt 1 X 2 0 Is A Y 1




A Show That The Given Differential Equation Has A Regular Singular Point At X 0 B Determine The Indicial Equation The Recurrence Relation And The Roots Of The Indicial Equation C Find The Series Solution X 0 Corresponding
(1x^2)y' 2xy = 0 The solution is listed at the back of the book as 9 y = C(1x^2) I double checked to make sure the problem and solution were right #10 dynamicsolo Homework Helper 1,648 4 For itex y = C ( 1 x^{2} ) /itex , the derivative is itex y' = C \cdot 2x /itex , yes?`y' (1x^2)y' 2xy = 0` Solve the differential equation 1 Educator answer Math Latest answer posted at AM(a) 4xy′′ 2y′ y = 0;




How To Solve This Differential Equation Math 1 X 2 Y 6xy 4y 0 R T Math Quora




4 A Solve The Differential Equation 1 X 2 Y 2xy L L 1 Y 0 Using Power Series Centered At 0 In Which Homeworklib
This answer uses an approach involving an integrating factor rather than separation of variables mathy'2xy=0 /math Note that the integrating factor, math\mu/math, takes on the form of e raised to the integral of the coefficient in frontStepbystep Solution Problem to solve ( 1 x 2) y ′ − 2 x y = 0 \left (1x^2\right)y'2xy=0 (1 x2)y′ −2xy = 0Popular Problems Calculus Find dy/dx 2xyy^2=1 2xy − y2 = 1 2 x y y 2 = 1 Differentiate both sides of the equation d dx (2xy−y2) = d dx (1) d d x ( 2 x y y 2) = d d x ( 1) Differentiate the left side of the equation Tap for more steps By the Sum Rule, the derivative of 2 x y − y 2 2 x y y 2 with respect to x x is d d x 2
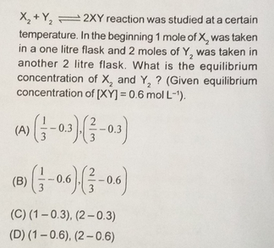



X2 Y2 2xy Reaction Was Studied At A Certain Temperature In Scholr




Pdf Ism T11 C03 C Pdf Samuel Boroni Academia Edu
We can use an integrating factor when we have a First Order Linear nonhomogeneous Ordinary Differential Equation of the form;Combine all terms containing x \left (y1\right)x^ {2}\left (y1\right)xy1=0 ( y − 1) x 2 ( − y − 1) x − y − 1 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute y1 for a, y1 for b, and y1 for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a} Ex 96, 8 For each of the differential equation given in Exercises 1 to 12, find the general solution (1𝑥^2 )𝑑𝑦2𝑥𝑦 𝑑𝑥=cot〖𝑥 𝑑𝑥(𝑥≠0)〗 Given equation (1 x2)dy 2xy dx = cot x dx Dividing both sides by dx (1 x2)𝑑𝑦/𝑑𝑥 2xy 𝑑𝑥/𝑑𝑥 = cot x 𝑑𝑥/𝑑𝑥 (1 x2)𝑑𝑦/𝑑𝑥 2xy = cot x Dividing bo



The Normal To The Curve X 2 2xy 3y 2 0 At 1 1 Sarthaks Econnect Largest Online Education Community



2
2 can be anything and the solution is y = csinx, otherwise sinL 6= 0 ,so c 2 = 0 and the only solution is y = 0 5 y00 y = x,y(0) = 0,y(π) = 0 First solve the homogeneous equation y00 y = 0r2 1 = 0,so r = ±i,so y = c 1 cosxc 2 sinx This is the general solution of the homogeneous equation Now,we look for a particular solution{eq}(1 x^2)y'' 2xy' 2y=0, {/eq} into a Maclaurin series to get a recurrence relation for the coefficients of the solution series By selecting appropriately the first two coefficients we'llExample Solve y00 2y0 y = 0 by the power series method Many special functions are de–ned as power series solutions to di⁄erential equations like (1) Legendre polynomials are solutions to Legendre™s equation (1 x2)y00 2xy0 n(n 1)y = 0 where n is a nonnegative integer Bessel functions are solutions to Bessel™s equation




Show That The General Solution Of The Differential Equation Dy Dx Y 2 Y 1 X 2 X 1 0 Is Given By X Y 1 A 1 X Y 2xy Where A Is Parameter Mathematics Shaalaa Com




Consider The Equation 1 X 2 Y 2xy 12y 0 Chegg Com
Steps Using the Quadratic Formula = { x }^ { 2 } { y }^ { 2 } 2xy1=0 = x 2 y 2 − 2 x y − 1 = 0 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions,Y(x) = X n=0 ∞ a n xn (19) 2 Substitute into the equation and determine a n A recurrence relation – a formula determining a n using a i, i2 Find the real numbers r such that y = ex is a solution of y00 8y0 16y = 0 Answer r = −4 3 Find the real numbers r such that y = ex is a solution of y00 −2y0 10y = 0 Answer There are no real numbers such that erx is a solution 4 Find the real numbers r such that y = xr is a solution of x2y00 − 5xy0 8y = 0 Answer r = 2, 4 5



Solved Solve The Following Differential Equations X Y 3 Dx X Y 1 Dy 0 2 X Y 1 Dx 3x 4y 2 Dy C 3 1 Y 2 Xy 2 Dx X 2y Y 2xy Dy Course Hero



Solve The Following Differential Equation 1 X 2 Dy Dx 2xy 1 1 X 2 Given Y 0 When X 1 Sarthaks Econnect Largest Online Education Community
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge andDy dx P (x)y = Q(x) We have y' − 2xy = 1 with y(0) = y0 1 This is a First Order Ordinary Differential Equation in Standard Form So we compute and integrating factor, I, using; 1 Alpha identifies it as Legendre's equation and gives the solution y(x) = c1x c2( − x(log(1 − x) / 2 − log(x 1)) − 1) It offers step by step if you have the right account Share answered Jul 19 ' at 1348 Ross Millikan




Differential Equations Variation Of Parameters X 2y 2xy 2y X Ln X Youtube




Giải Hệ Phương Trinh X 2 Y 2 2xy 1 Va 2x 2 2y 2 2xy Y 0 Toan Học Lớp 9 Bai Tập Toan Học Lớp
Get an answer for '`y' (1x^2)y' 2xy = 0` Solve the differential equation' and find homework help for other Math questions at eNotesI think it's reasonable to do one more separable differential equation from so let's do it derivative of Y with respect to X is equal to Y cosine of X divided by 1 plus 2y squared and they give us an initial condition that Y of 0 is equal to 1 or when X is equal to 0 Y is equal to 1 and I know we did a couple already but another way to think about separable differential equations is really allSection 62, #9 Solve (1x2)y'−2xy=0 (1 ) 2 ' x2 xy y = (1 ) 2 x2 xy dx dy = dy(1x2)=2xydx y xydx y dy(1 x2) 2 = x dy xdx y 1(1 2) =2 ∫ ∫



Q Tbn And9gcqqdjererih8cbajqv Puntih4ikbw7iy9bdv7cgyhxgixkwubp Usqp Cau




Second Solution For Reduction Of Order X 2 1 Y 2xy 2y X 2 1 Youtube
(b) 2xy′′ (3−x)y′ − y = 0 Solution (a) Write the differential equation in standard form y′′ − 1 2x y′ 1 4x y = 0 We have P(x) = − 1 2x and Q(x) = 1 4x, so x = 0 is a singular point Taking limits we get lim x→0 xP(x) = −1/2 and lim x→0 x2Q(x) = 0 Therefore xSolve the Differential Equation (x^21)y'=xy In this tutorial we shall solve a differential equation of the form ( x 2 1) y ′ = x y by using the separating the variables method The differential equation of the form is given as ( x 2 1) y ′ = x y This differential equation can also be written as ( x 2 1) d y d x = x y Solution From Theorem 1111, λ = 0 is an eigenvalue of Equation 1115 with associated eigenfunction y0 = 1, and any other eigenvalues must be positive If y satisfies Equation 1115 with λ > 0, then y = c1cos√λx c2sin√λx, where c1 and c2 are constants




Misc 7 Show That General Solution Is X Y 1 A 1 X Y 2xy




Show Function F X Y X 2 Y 2 2xy Is 1 1 By Inverse Function Theorem Mathematics Stack Exchange
Letting y(x) = Q(q) and noting that sin2 q = 1 x2, Equation (11) becomes d dx (1 x2) dy dx l m2 1 x2 y = 0(14) We further note that x 2 1,1, as can be easily confirmed by the reader This is a SturmLiouville eigenvalue problem The solutions consist of a set of orthogonal eigenfunctions For the special case that m = 0 Equation (14 #y_O =x sum_1^oo (1)^(k) (3* 7 * * (4 k 1))/((2k1)!) x^((2 k1)) # Recognising the linearity #y = c_1\ y_O c_2 \ y_E# So you have to add all that up Finally, a screen grab from Socratic that always puts me of answering qu's like this in proper fashion I'd recommend this147 7 f(x;y) = (x y)(1 xy) = x y x2y xy2)f x = 1 2xyy2;f y = 1 x22xy;f xx = 2y;f xy = 2x2y;f yy = 2x Then f x = 0 implies 1 2xyy2 = 0 and f y = 0 implies 1 x22xy = 0 Adding the two equations gives 1y2 1 x2 = 0 )y2 = x2)y = x, but if y = x then f x = 0 implies 12x2 x2 = 0 )3x2 = 1 which has no real solution If y = x then substitution into f




Answered 7 Y 9 Xy Y Vx 11 Xy 2y X X 0 Bartleby




Bt Ptvp Xuan Sv Moi
Solution for X^22xyy^22x1=0 equation Simplifying X 2 2xy y 2 2x 1 = 0 Reorder the terms 1 X 2 2x 2xy y 2 = 0 Solving 1 X 2 2x 2xy y 2 = 0 Solving for variable 'X' Move all terms containing X to the left, all other terms to the right Add '1' to each side of the equation 1 X 2 2x 2xy 1 y 2 = 0 1 Reorder the terms 1 1 X 2 2x 2xy(1 2x)y00 2xy0 y= 0;Y′′(x) = X∞ n=2 n(n −1)c nxn−2 If we plug these into the ODE we get X∞ n=0 n(n − 1)c



Www3 Nd Edu Apilking Math Work Old exams Exam2f07solutions Pdf



Www Tau Ac Il Levant Ode Solution 6 Pdf
Legendre's equation(1 x2)y00 2xy0 n(n 1)y = 0 Used for modeling spherically symmetric potentials in the theory of Newtonian gravitation and in electricity & magnetism (eg, the wave equation for an electron in a hydrogen atom) Parametric Bessel's equation x2y00 xy0 ( x2 2)y = 0 Used for analyzing vibrations of a circular drum(1 x2)y00 xy0 2y= 0 where is a constant, is called the Chebyshev quatione (a) Compute two linearly independent series solutions for jxjPutting this into the lefthand side of




Show That The General Solution Of The Differential Equation Dy Dx Y 2 Y 1 X 2 X 1 0 Is Given By X Y 1 A 1 X Y 2xy Where A Is Parameter Mathematics Shaalaa Com




Power Series
And therefore the solution y(x) contains only even powers of x Using the Ratio Test, it can be determined that the series converges for all x However, if we let j= 2n, since only even powers are included, then we nd that for su ciently large n, a 2n2 =(x2 − 1)y′′ 4xy′ 2y = 0 State the recurrence relation and the guaranteed radius of convergence Solution A power series solution y(x) and its derivatives will have the forms y(x) = X∞ n=0 c nx n;Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history




Engineering Mathematics Notes




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When
Y'' 2xy = 0 Extended Keyboard;



Www Ualberta Ca Csproat Homework Math 334 Assignment solutions Assignment 6 solutions Pdf




Use The Reduction Of Order Method To Solve The Following Problem Given One Of The Solution Y1 A X 2 1 Y 39 39 2xy 39 2y 0 Y1 X B 2x 1 Y 39 39 4 X 1 Y 39 4y 0 Y1 E 2x C X



Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 6y 0 Stumbling Robot




Differential Calculus Concepts Problems 126 Rd 1 Matrix




Integer Solutions Rational Solutions Of The Equations X4 Y4 Z4 2x2y2 2y2z2 2z2x2 N



Solve The Following Differential Equation X2 Y2 Dx 2xy Dy 0 Given That Y 1 When X 1 Or Solve The Following Differential Equation If Y 1 When X 1 Mathematics Topperlearning Com 237hoo



1 X Y Y 2 Differential Equation




Ma 17 3 Complex Analysis Rates




Power Series




Show That The Equation 5x4 3x2y2 2xy3 Dx 2x3y 3xy2 5y4 Dy 0 Is An Exact Differential Equation Find Its Solution Mathematics 2 Question Answer Collection




Consider The Following Equation X 2 1 Y 2xy Chegg Com
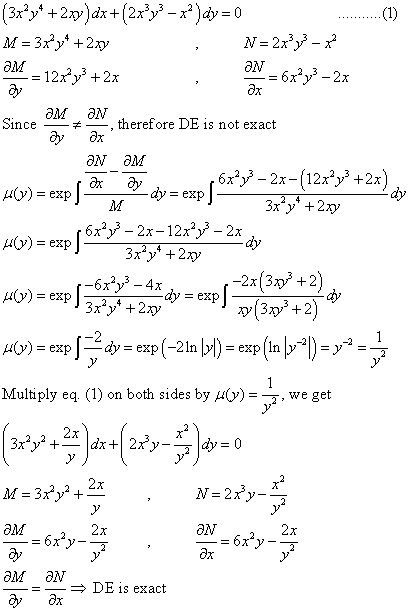



Differential Equations Solved Examples Show That Following Differential Equation Is Not Exact 3x 2y 4 2xy Dx 2x 3y 3 X 2 Dy 0 Then Find An Integrating Factor To Solve The Differential Equation



Http Www Math Miami Edu Dscheib Teaching Fall11 Map2302 Files Map2302 Quizzes Exams Files Exam4 Answers Pdf




X 2 Y 2 Dx 2xy Dy 0 Integrating Factor Novocom Top




Answered Reduce To First Order And Solve 1 Bartleby



2




Y 2xy E X Dx E Xdy 0 Novocom Top
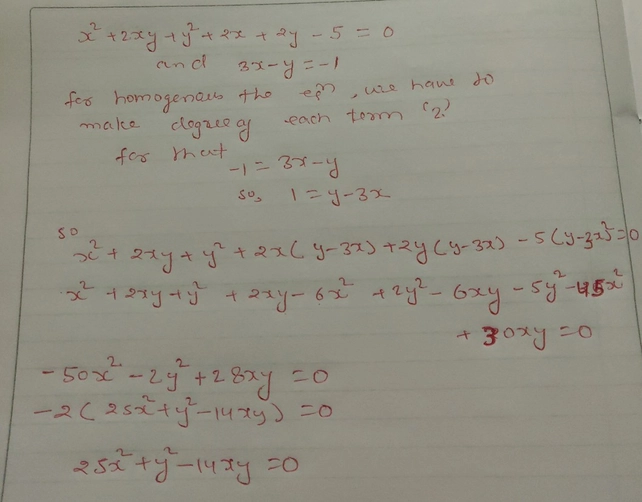



3 Bar7 1 Tal X22xyy22times L See How To Solve It At Qanda




First Order Differential Equations Ppt Download



Anfangswertproblem Y 2xy 1 X 2 Y 0 3 Losen Differentiale Mathelounge



Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 12y 0 Stumbling Robot




Ex 9 6 14 Find Particular Solution 1 X2 Dy Dx 2xy



If X Sin T And Y Sin Pt Prove That 1 X2 D2y Dx2 Dy Dx P2y 0 Studyrankersonline



Http Www Math Miami Edu Dscheib Teaching Fall11 Map2302 Files Map2302 Suggested Homework Problems Files Section 3 1 hw Pdf



Solve The Following Differential Equation X2 Y2 Dx 2xy Dy 0 Given That Y 1 When X 1 Or Solve The Following Differential Equation If Y 1 When X 1 Mathematics Topperlearning Com 237hoo



Hw 4




Answered The General Solution For Legendre Bartleby



Search Q X 2b2y 3d0 Graph Tbm Isch




1 Find A Series Solution Of X 4 Y 2xy 12y Chegg Com
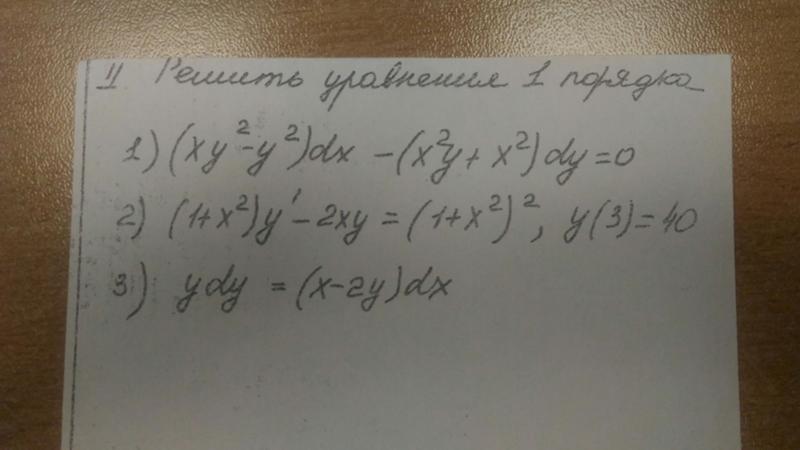



Otvety Mail Ru Reshenie Uravneniya 1 Poryadka 1 Xy 2 Y 2 Dx X 2y X 2 Dy 0 2 1 X 2 Y 2xy 1 X 2 2 Y 3 40 3 Ydy X 2y Dx



Solved Find The Power Series Solution Of The Differential Equation About An Ordinary Point X 0 1 X2y 2xy 2y 0 Why We Find Power Series Soluti Course Hero




Find A Power Series Solution In Powers Of X Show The Details 1 X Y 2xy 2y 0 Homework Help And Answers Slader




Power Series Solution To Y 2xy 0 Mathematics Stack Exchange




1 2e X Y Dx 2e X Y 1 X Y Dy 0 Novocom Top




Chebyshevs Differential Equation Math Assignment Docsity




1 X 2 Y 2xy 0 Reshit Differencialnoe Uravnenie



Matematikcimehmetyavuz Files Wordpress Com 15 04 M V Makarets V Yu Reshetnyak Ordinary Diffe Pdf




1a Engineering Mathematics Ppt Download




What Curves Are Represented By The Equation X2 2xy 1 Y2 2 Y 1 0 For Different Values Of Lamda Brainly In
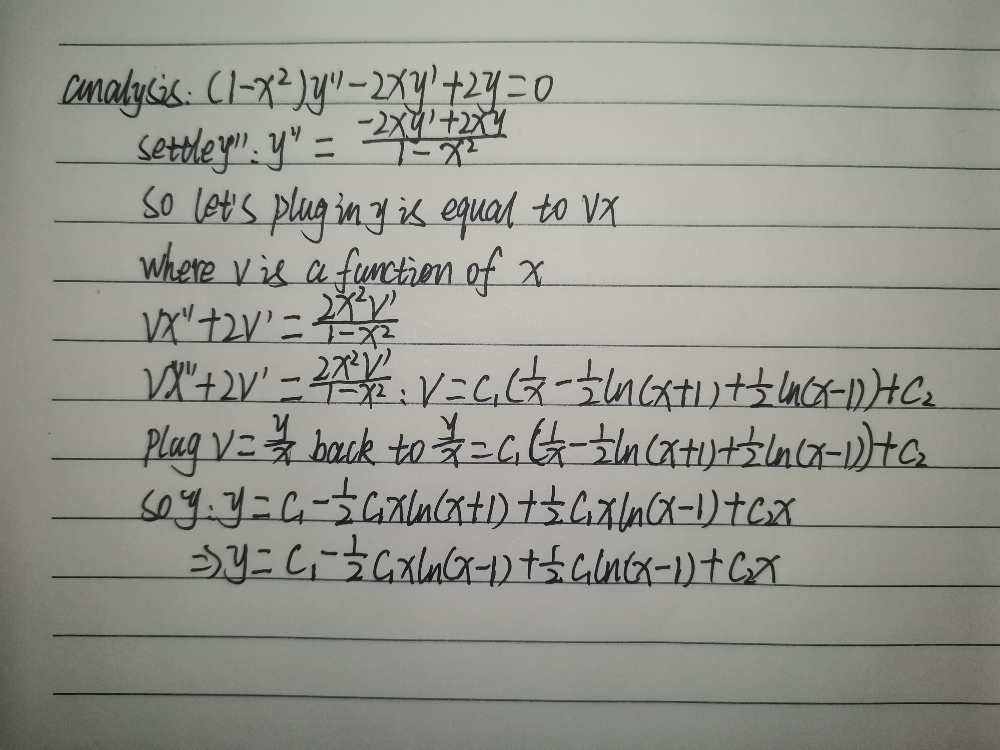



1 X2y 2xy 2y 0 Gauthmath




Iit 04 Find Y 0 If Y Is A Function Of X And Ln X Y 2xy 0 Youtube




Ex 9 6 8 Find General Solution 1 X2 Dy 2xy Dx Ex 9 6




Solve 1 X 2 Y 2xy 2y 0 Via Simple Chegg Com



Ocw Mit Edu Courses Mathematics 18 075 Advanced Calculus For Engineers Fall 04 Assignments Sol 7 Fall 04 Pdf



Http Www Math Boun Edu Tr Personal Archives Arsiv2 2pdfler 2y01mt1 Pdf



Solved Let Y Dy Dx The Derivative On X 1 X 2 Y 2xy F X Where F X Is A Piece Wise Defined Function By F X X If X 0 1 And F X




Miscellaneous Problems Differential Equations




Solved If Y1 X Y2 X2 Are Two Linearly Independent Courses Archive




3 2 Problems Find General Solutions In Powers Of X Of The Diferential Equa Tions In Problems 1 T Homeworklib




If Y Tan 1x Show That 1 X2 Y 2xy 0 Maths Inverse Trigonometric Functions Meritnation Com



Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 6y 0 Stumbling Robot



2




Answered Reduce To First Order And Solve 1 Bartleby




What Is The Solution Of X 3y X 2y 2xy 2y 0 Quora




Prove That U X 2 Y 2 2xy 2x 3y Is Harmonic And Find Harmonic Conjugate V Edurev Iit Jam Question




We Observe That The Caachy Ri See How To Solve It At Qanda




Hyers Ulam Stability Of Differential Equation Y 2xy 2ny 0 Topic Of Research Paper In Mathematics Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub



Mathfunc




Given 1 X 2 Y 2xy 12y 0 Find A All Chegg Com




Find A Series Solution About The Point X 0 Of 1 X 2 Y 2xy 2y 0 Youtube




Givenof Solve The Equation 1 X 2 Y 2xy 2y 0 Giventhat Y X Is A Solution Brainly In
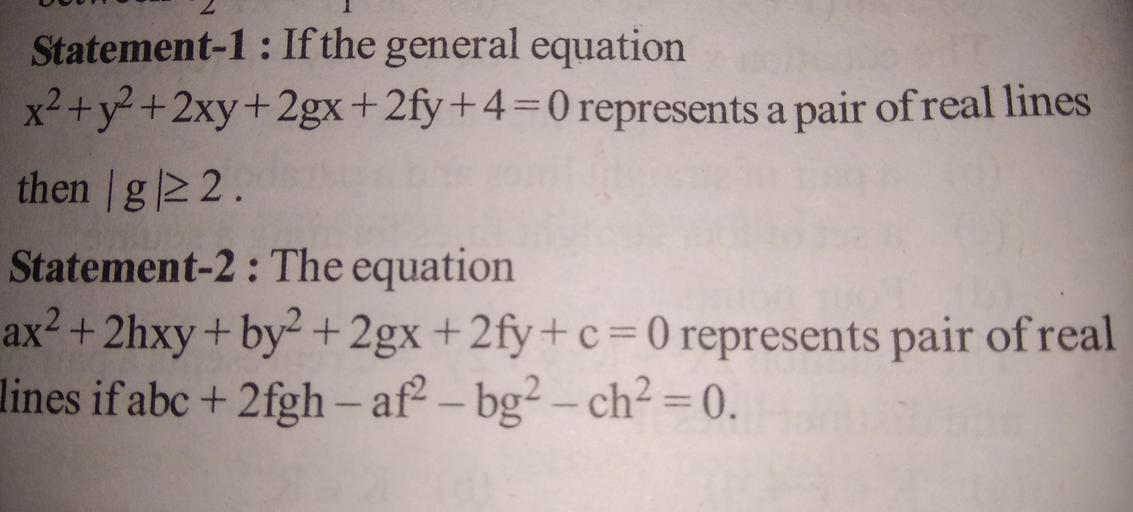



Statement 1 If The General Equation X2 Y2 2xy 2gx Math




Otvety Mail Ru Pomogite Reshit 1 X 2 Y 2xy 1 X 2 2 Y 0 1 Poyasnenie Vozvedenie V Stepn




Polynomial Solution Of The Equation 1 X 2 Y 2xy 6y 0 Mathematics Stack Exchange



Solve 1 X 2 Dy Dx 2xy 4x 2 0 Subject To The Initial Condition Y 0 0 Sarthaks Econnect Largest Online Education Community




The Solution Of Dy Dx X 2 Y 2 1 2xy Satisfying Y 1 0 Is




Math 432 Hw 2 5 Solutions Pdf Free Download



1
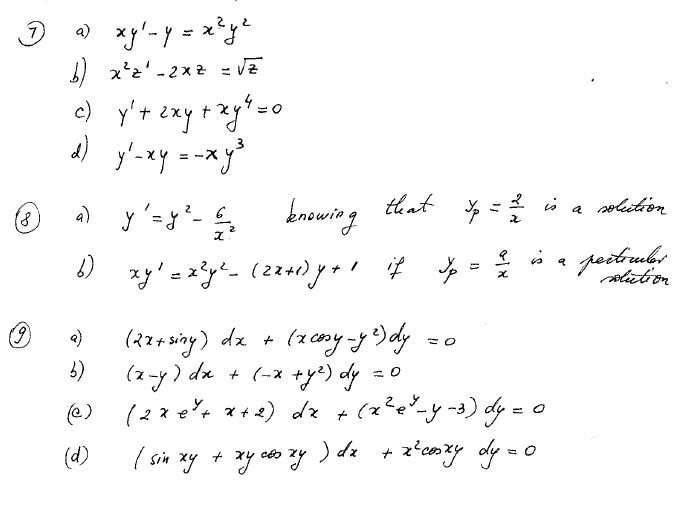



Privado Results



Www Jstor Org Stable




If Y Y X Is The Solution Of The Differential Expuation X Frac Partial Y Partial X 2 Y X 2 Satisfying Y 1 1 Then 16 Y 1 2




What Is The Solution To The Differential Equation Math 1 X 2 Y 2xy 2y 0 Math Quora




Solutions To Implicit Differentiation Problems
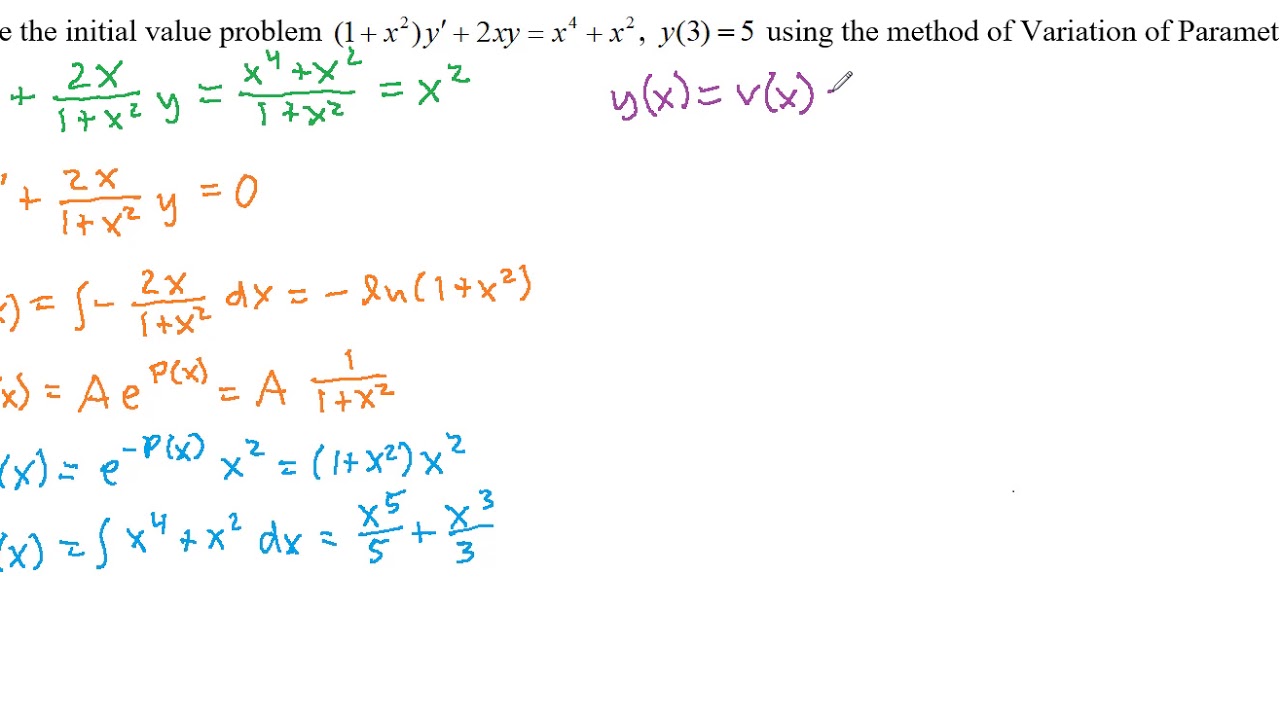



First Order Linear Differential Equations



0 件のコメント:
コメントを投稿